机器学习概述
机器学习(Machine Learning,ML)是实现人工智能的一种方法,它来源于早期的人工智能领域,是人工智能研究发展到一定阶段的必然产物。机器学习可以分为以支持向量机为代表的统计学习和以人工神经网络为代表的深度学习。统计学习模型参数往往是可解释的,而人工神经网络则是一个“黑箱”。
本章我们首先主要介绍统计机器学习,包括机器学习的发展和基本实现方法,然后引出自动化机器学习。
3.1 机器学习的发展
3.1.1 “机器学习”名字的由来
人工智能在1956年由约翰·麦卡锡(John McCarthy)首次定义,其含义是可以执行人类智能特征任务的机器。包括语言理解、物体识别、声音识别、学习和智能地解决人类问题等方面。人工智能可以从广义和狭义两个方面理解:广义是指人工智能是可以实现同等人类能力的计算机;狭义是指其可以做人类要求的特定任务,并且能够做得非常好,比如一台用来识别图像的机器就仅限于能够很好地识别图像,而不能做其他事情。
机器学习是人工智能的核心任务,阿瑟·塞缪尔(Arthur Samuel)将机器学习定义为“没有明确编程就能学习的能力”。虽然在不使用机器学习的情况下,就可以实现人工智能,但是这需要通过定义复杂的规则和决策树等方式来构建数百万行代码。因此,就出现了现在的机器学习算法,不需要通过手动编码和定义特定的指令来完成特定的任务,只需要以一种“训练”算法的方式让机器自己学习,并根据输入的数据进行自我调整和改进。
那么“机器学习”的名字是怎么来的呢?
1952年,阿瑟·塞缪尔在IBM公司研制了一个西洋跳棋程序,塞缪尔自己并不是下西洋棋的高手,因此这个计算机程序的下棋能力很差,但是它具有自学习能力,可以通过自己对大量棋局的分析,逐渐学会如何分辨当前局面出的是“好棋”还是“坏棋”,从中不断积累经验和吸取教训,进而不断提高棋艺,最后竟然超过了塞缪尔本人。塞缪尔认为,在不使用具体的代码,只使用一定数量的训练数据和泛型编程的前提下,机器就可以从训练数据中学到赢棋的经验,这就是机器学习最初的定义。1961年,“知识工程之父”爱德华·费根鲍姆(Edward Feigenbaum,1994年图灵奖得主)为了编写其巨著《Computers and Thought》,邀请塞缪尔提供该程序最好的一个对弈实例。借此机会,塞缪尔向当时的康涅狄格州的跳棋冠军,也是全美排名第四的棋手发起挑战,最终塞缪尔的程序获得了胜利,轰动一时。
塞缪尔的这个跳棋程序不仅在人工智能领域成为经典,它还推动了整个计算机科学的发展进程。计算机刚出现的时候,只是被用来做大型计算的机器,不可能完成没有事先编好程序的任务,而塞缪尔的跳棋程序,打破了这种思想的禁锢,创造了不可能,从那以后,引领了新的计算机潮流,成为后人发展计算机的新方向。
3.1.2 “机器学习”的前世今生
20世纪50年代到70年代初期,人工智能在此期间的研究被称为“推理期”,简单来说,人们认为只要赋予机器逻辑推理能力,机器就能具有智能。这一阶段的代表性工作有A. Newell和H. Simonde的“逻辑理论家”(Logic Theorist)程序,以及后来的“通用问题求解”(General Problem Solving)程序等,这些工作在当时获得了令人振奋的结果。“逻辑理论家”程序分别在1952年和1963年证明了著名数学家罗素和怀特海的名著《数学原理》中的38条定理和全部的52条定理。因此,A. Newell和H. Simonde成为1975年图灵奖的获得者。随着研究的深入发展,机器仅仅具有逻辑推理能力是远远不够的,为了实现人工智能,机器必须要具有智能,也就是说,必须要想办法让机器拥有知识。
从20世纪70年代中期开始,人工智能的研究就进入了“知识期”。1965年,Edward Feigenbaum主持研制了世界上第一个专家系统“DENDRAL”,自此开始,一大批专家系统成为主流,它们也在很多应用领域取得了成功。因此,在1994年Edward Feigenbaum获得了图灵奖。但是,专家系统随着科学技术的进步,面临了“知识工程瓶颈”,最大的困境就是,由人把知识总结出来再教给计算机是相当困难的。那么,让机器自己学习知识,会不会成为可能呢?
答案是肯定的,有太多的事实已经证明机器是可以自己学习知识的,其中最早的是上文提到的塞缪尔的跳棋程序。到20世纪50年代中后期,出现了基于神经网络的“联结主义”(Connectionism)学习,代表作是F. Rosenblatt的感知机(Perceptron)、B. Widrow的Adaline等。在20世纪六七十年代,多种学习技术得到了初步发展,基于逻辑表示的“符号主义”(Symbolism)学习逐渐发展,例如以决策理论为基础的统计学习技术以及强化学习技术等。二十多年后,“统计机器学习”(Statistical Learning)迅速崛起,代表性的技术有支持向量机(Support Vector Machine,SVM)等。
在过去的二十多年中,人类在收集数据、存储、传输、处理数据上的需求和能力得到了很大的提升。随着大数据时代的到来,人类社会无时无刻不在产生着数据,那么如何有效地对数据进行分析和利用,成为迫切需要解决的问题,而机器学习恰巧成为有效的解决方案。目前,在人类生活的各个领域,都可以看到机器学习的身影。无论是在复杂的人工智能领域,如自然语言处理、专家系统、模式识别、计算机视觉、智能机器人,还是在多媒体、网络通信、图形学、软件工程、医学领域,甚至是更常见的购物系统等,机器学习已然成为我们不可获取的一部分。
有关机器学习的介绍已经非常多了,在这里就不再赘述,我们接下来的讲述重点将放在机器学习的实现方法,还有为了解决现有机器学习的问题,而产生的自动化机器学习到底是什么吧。
3.1.3 “机器学习”的理论基础
在机器学习发展的过程中,逐渐分划成两条路线,这同时也影响了后来的自动化机器学习。一条路线是以Barlow为主导的单细胞学说,这个理论是说,一开始是从零基础开始的,一个单细胞逐渐发展生长出多个细胞,这也意味着神经细胞的结构可能会很复杂。而另一条路线是Hebb主张的,由多个相互关联的神经细胞集合体作为开始,称其为ensemble,并不断通过改变细胞个数和细胞间的连接来发展神经细胞的结构。虽然这两种假设都有生物学证据的支持,但是至今没有生物学的定论,这也为计算机科学家们提供了想象的空间,也造就了后来机器学习发展过程的不同研究路线,并且这两种假设都对机器学习研究有相当重要的引导作用。
基于这两种假设,机器学习的发展历程被分为了两类,一类是以感知机、BP和SVM等为主导的,另一类是以样条理论、K-近邻、符号机器学习、集群机器学习和流形机器学习等代表的。
本书中的重点—统计机器学习是近几年被广泛应用的机器学习方法。从广义上说,这是一类方法学。当我们从问题世界观测到一些数据,如果没有能力或者没有必要建立严格的物理模型时,可以使用数学方法从这些数据中推理出数学模型。注意,这里的数学模型一般是没有详细的物理解释的,不过会在输入输出的关系中反映实际问题,这就是我们开始提到的“黑箱”原理。一般来说,“黑箱”原理是基于统计方法的,统计机器学习的本质就是“黑箱”原理的延续。因此,统计机器学习主要关注的是数学方法的研究,而神经科学则被列为深度学习领域。
统计机器学习的基本要求是,假设同类数据具有一定的统计规律性。目标则是,从假设的空间中,也就是常说的模型空间,从输入空间到输出空间的映射空间中寻找一个最优的模型。综上,可以总结统计机器学习方法的主要研究问题,可分为如下3个:
1)模型假设:模型假设要解决的问题是如何将数据从输入空间转化到输出空间,通常用后验概率或是映射函数来解决。
2)模型选择:在模型的假设空间中,存在无穷多个满足假设的可选择模型,模型选择要解决的问题就是如何从模型假设空间中选择一个最优模型。通常采用损失函数来指定模型选择策略,将模型选择转化为一个最优化问题来求解。为了降低模型的复杂性,提高模型的泛化能力,避免过拟合的发生,通常会加上正则化项。
3)学习算法:既然已经将模型选择转化为一个最优化问题了,那么最优化问题该如何实现,这就是学习算法要解决的了。比如在给定损失函数后,并且在损失函数的约定条件下,怎样快速地找到最优解,常用的学习算法包括梯度下降等。
统计机器学习的这3个问题都是机器学习发展过程中的研究热点。对于模型假设来说,如果模型选择错误,那么无论如何都难以描述出数据集的正确分布特性。从而,在模型空间假设上,衍生出了很多方法,包括交叉验证等。模型选择的关键问题在于损失函数的设计,损失函数通常包括损失项和正则化项,不同的选择策略会造成不同的模型选择,而模型选择的不同,则会导致预测效果的巨大差异。对于学习算法来说,不同的学习算法,其学习的效率会有很大的差异,而且学习出来的效果也不一样。
统计机器学习是基于对数据的初步认识以及学习目的的分析(特征工程),选择合适的数学模型,拟定超参数,并输入样本数据,依据一定的策略,运用合适的学习算法对模型进行训练,最后运用训练好的模型对数据进行分析预测。具体流程如图3-1所示。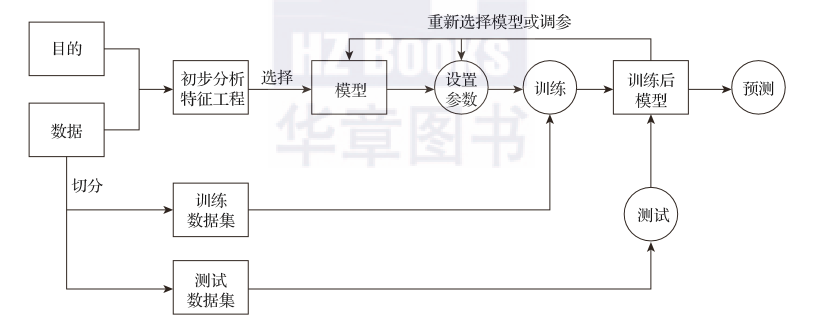
图3-1 统计机器学习的流程图
根据图3-1中的流程和统计机器学习研究的3个主要问题,可以将统计机器学习总结为如下3个要素:
1)模型(model):比如支持向量机、人工神经网络模型等。模型在未进行训练前,其可能的参数是多个甚至无穷的,故可能的模型也是多个甚至无穷的,这些模型构成的集合就是假设空间(hypothesis space)。
2)策略(strategy):即从假设空间中挑选出参数最优的模型的准则。模型的分类或预测结果与实际情况的误差(损失函数)越小,模型就越好。
3)算法(algorithm):即从假设空间中挑选模型的方法(等同于求解最佳的模型参数)。机器学习的参数求解通常都会转化为最优化问题,例如支持向量机实质上就是求解凸二次规划问题。
3.2 机器学习的实现方法
机器学习的核心是“使用算法解析数据,从中学习,然后对世界上的某件事情做出决定或预测”。这意味着,与其显式地编写程序来执行某些任务,不如教计算机如何开发一个算法来完成任务。机器学习主要可以分为3个类型:监督学习、非监督学习和强化学习。我们在这里仅介绍监督学习和非监督学习,强化学习的内容请参考第9章。
监督学习要求数据必须被标记过,计算机可以通过使用特定的模式来识别被标记的样本。监督学习可以分为两种类型:分类和回归。分类,即机器被训练来完成对一组数据进行特定的分类。生活中最常见的一种分类问题是垃圾邮件的分类。机器首先分析以前被用户标记为垃圾邮件的类型、特征等,然后将新邮件与这些曾被标记为垃圾邮件的邮件进行对比,根据设定的匹配度来做决定。假设将匹配度的阈值设为90%,即表示匹配度大于或等于90%的邮件被分类为垃圾邮件,而匹配度小于90%的邮件被认为是正常邮件。回归,即机器根据先前(标记)的数据来预测未来。天气预测是最好的回归例子,根据气象事件的历史数据(平均气温、湿度和降水量)和当前天气的数据,对未来的天气进行预测。
无监督学习,其数据是不需要被标记的,在我们的现实世界中的数据大多数也都是不带标签的,标记数据会浪费大量的人力物力,因此这类算法是非常有用的。无监督学习主要分为聚类和降维。聚类是指,根据数据的特征和行为对象进行分组,这里说的分组与分类算法是不同的,分类算法的组是人为规定的,而聚类算法中的组,则是由计算机自定义的,不是人为规定。聚类,将一组数据划分成不同的子组,如年龄、性别这样的特性,然后再将其应用到特定问题中。降维,则是通过找到数据间的共同点,来减少数据集的变量,减少冗余的发生。降维也是后文将会提到的特征工程中的一个重要方面。
下面我们将逐一介绍机器学习中一些经典问题,分别是分类问题、回归问题和聚类问题。
3.2.1 分类问题
在机器学习中,最常见的问题就是分类问题了。所谓分类问题,就是对输入数据,进行分类。通常,将能够完成分类任务的算法,称为分类器(Classifier)。即找到一个函数判断输入数据所属的类别,可以是二分类问题(是或不是),也可以是多分类问题(在多个类别中判断输入数据具体属于哪一个类别)。分类问题的输出值是离散的,其输出结果是用来指定其属于哪个类别。
分类问题的求解过程可以分为以下3个步骤:
1)确定一个模型,输入样本数据,最后输出其类别;
2)定义损失函数;
3)找出使损失函数最小的那个最优函数。
通过这种方法,可以直接计算出寻找到的最优函数,即样本属于每个类别的概率,这种方法被称为判别式(Discrimination)方法,因为其可以直接对样本所属类别进行判断,相应的模型也可以称为判别式模型。如果借助概率论的知识,分析每一类的特征,这样就可以将二分类问题应用到多分类问题中。以最简单的二分类为例,建模,使用条件概率,进行如下转换: 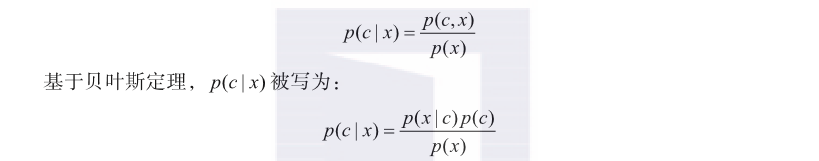
对于给定的样本数据,与类别无关,因此只需要考虑和,这两个分布正好是每一类样本的特征,因此只对这两个分布进行研究。
是类先验概率,即在未知其他条件下对事件发生概率的表示,这个值是通过以往经验和分析(历史数据)得到的结果。根据大数定律,当训练样本中包含充足的独立同分布样本时,可以通过各类样本的出现频率进行估计;与类先验概率相对应的是类后验(Posterior)概率,即需要建模的目标,表示在已知条件下事件发生的概率。
是类条件(class-conditional)概率,即在某个特定类别下,样本的发生概率。它是涉及关于样本所有特征的联合概率,如果有个特征且取值均为二值,那么样本空间大小将是,现实中训练样本的大小往往远小于这个值,因此通过频率估算显然是不可行的,因为“未被观测到”不等于“出现概率为0”。那么就需要应用其他方法进行求解了,如高斯分布、极大似然估计、朴素贝叶斯分类等。
1.高斯分布
通常,假定类条件概率符合某种确定的概率分布,训练样本都是从这个分布中随机采样得到的,“未被采样到的点”也对应一个发生概率。某种确定的概率分布通常被假设为高斯分布(Gaussian Distribution),现在就需要根据训练样本确定高斯分布的参数。多元高斯分布的概率密度函数如下: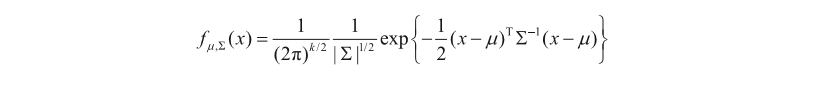
其中是的维数,是均值向量,是协方差矩阵,决定了分布的最高点,决定了分布的形状。
2.极大似然估计
任何一个高斯分布都可以采样出训练样本,但是分布的不同,采样出训练样本的可能性是不一样的,对给定和采样出训练样本的可能性可以写作: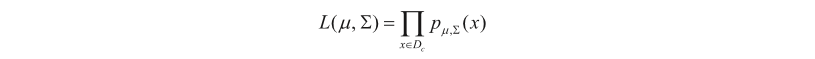
表示训练样本中属于类别的样本数目。最大化上面的似然函数,找出的和就是最佳参数。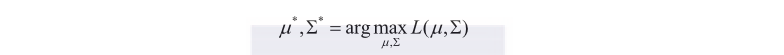
该方法被称为最大似然估计(Maximum Likelihood Estimation,MLE),参数和的最大似然估计为: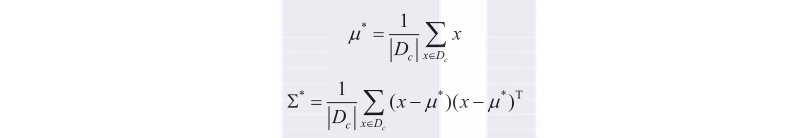
也就是说,最佳是样本均值,协方差矩阵是的均值。现在已经计算出每个类别的和,这样就可以选择较大的那个类别作为的类别。
3.朴素贝叶斯分类
如果假设样本的所有特征值都是相互独立的,那么可以写成: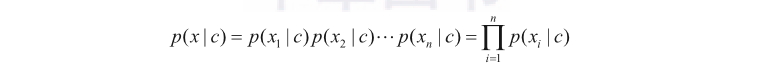
其中,是特征数目,是第个属性。同样可以假设每一维特征上的概率分布仍然服从高斯分布,此时的高斯分布是一个一维高斯分布,对应一个实值,组成协方差矩阵也只在对角线位置有值,进一步减少了参数数目,得到了更简单的模型。这样的模型被称作朴素贝叶斯分类器(Naive Bayes classifier,NB)。最后,对于样本分布不一定要选择高斯分布,例如如果是二值分布,可以假设符合伯努利分布,具体应用中要根据样本特点具体而定。
3.2.2 回归问题
回归(Regression)模型是指机器学习方法学到的函数的输出是连续实数值,它主要适用于预测问题,常见模型包括基础的线性回归模型和多项式回归模型。
线性回归
按照机器学习建模的3个步骤,首先需要确定选用的模型,基于问题我们很容易知道此处应使用线性回归(Linear Regression)模型,然后将其形式化表达: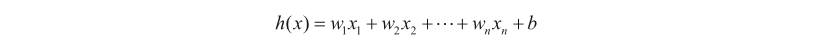
其中,是样本数据的维特征描述,每一组和能确定一个不一样的,和的所有取值组合就构成了可选函数集合,而回归任务要做的就是如何从这个函数集合中选出“最好”的那个函数。
对于训练数据集D描述如下: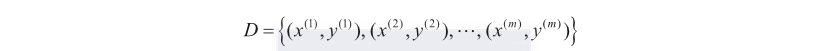
其中,是样本的维特征向量表示,是样本标记。线性回归的目标是学到一个线性函数以尽可能准确地预测实值输出标记。
因此需要确定一个衡量标准,来度量一个函数的好坏,这就需要损失函数(Loss Function)。根据线性回归的目标,只需要度量与之间的差距,均方误差(Mean Square Error,MSE)是回归任务中最常用的损失函数。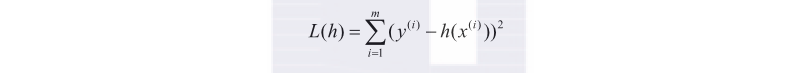
3.2.3 聚类问题
常见的聚类问题的算法当属k-means算法了,k-means算法的核心思想是簇识别。假定有一些数据,把相似数据归到一起,簇识别会告诉我们这些簇到底是什么。簇的个数是用户给定的,每一个簇都有一个“心脏”—聚类中心,也叫质心(centroid)。聚类与分类的最大不同是,分类的目标事先已知,而聚类则不知道分类标签是什么,只能根据相似度来给数据贴上不同的标签。相似度的度量最常用的是欧氏距离。k-means算法的基本流程如下:
1)给定输入训练数据: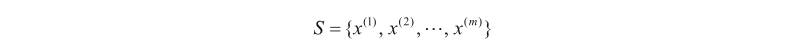
2)随机选择初始的k个聚类中心: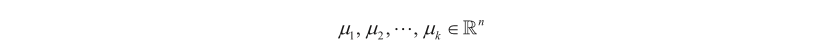
3)对每个样本数据,将其类别标号设为距离其最近的聚类中心的标号: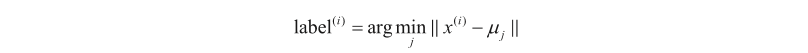
4)将每个聚类中心的值更新为该类别所有样本的平均值: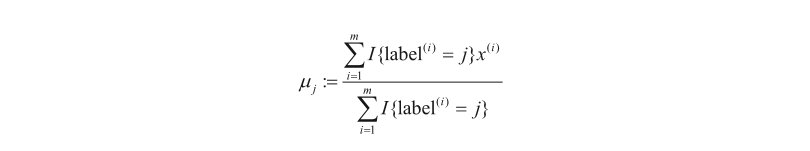
5)重复第3步与第4步,直到算法收敛为止,此时的聚类中心将不再移动。
k-means算法的优化目标函数表示如下: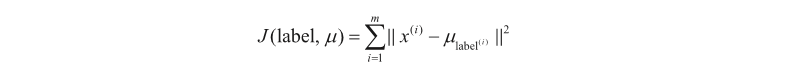
由于这个目标函数不是凸函数,因此不能保证算法会收敛到一个全局最优值,只能保证收敛到一个局部最优值。解决这个问题有两种方法:一是随机初始化多次,以最优的聚类结果为最终结果;二是二分k-means算法。
3.3 自动化机器学习
3.3.1 机器学习面临的问题
机器学习的步骤如图3-2所示,就一般情况而言,算法工程师的任务一般从特征工程开始。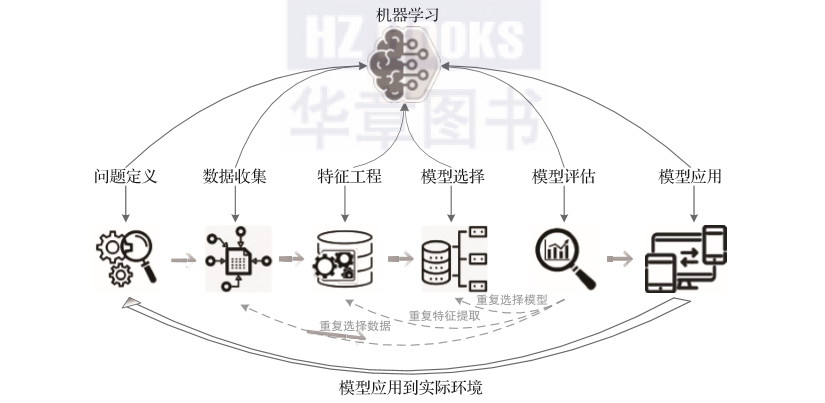
图3-2 机器学习知识图谱
特征工程是数据分析中最耗费时间精力的一部分工作,它不像算法和模型是确定的步骤,而大多情况下要依靠算法工程师的个人经验来处理。这样的特征工程具有很强的不确定性,如漏选特征、选到了无效特征、忽略高级特征等。漏选特征会造成信息的缺失,使模型效果变差;而加入了无效特征会让模型变大,增加了不必要的计算量;高级特征需要通过一般特征的运算来得到。还有其他问题,如缺失值、离散特征连续化、归一化、标准化、数据清洗等。
而在模型选择阶段,也需要依靠算法工程师的经验来做,算法工程师通常是根据特征工程后的数据来进行选择。
之后会进行模型评估阶段,通过模型评估来决定模型是否能运用在实际生产中。如果模型未能通过评估,就需要重新返工,重新进行数据收集、特征工程、模型选择过程。这是相当耗费时间的工作并且需要十分丰富的经验。在实际生产中,大多数情况下可能并不能生成理想的模型,并且会耗费大量的时间。
3.3.2 为什么会产生AutoML
为了解决上述问题而诞生了AutoML,AutoML试图将这些特征工程、模型选择以及参数优化等重要步骤进行自动化学习,使得机器学习模型无需人工参与即可被应用。
从前节可见,机器学习的泛化受到了诸多条件的制约,此时急需一种更加通用的方案来解决上述问题,这就产生了AutoML。AutoML是一个将从根本上改变基于机器学习解决方案现状的方案。
AutoML是一个控制神经网络提出一个可以在特定任务上训练和评测性能的子模型架构,测试的结果会反馈给控制器,让控制器知道下一轮如何改进自己的模型。自动机器学习集中在以下两个方面:数据采集和模型预测。在这两个阶段之间所有发生的步骤将被自动机器学习抽象出来。实际上,用户只需要提供自己的数据集、标签并按下一个按钮来生成一个经过全面训练的和优化预测的模型。大多数平台都提示用户来上传数据集,然后对类别进行标记。之后,在数据预处理、模型选择、特征工程和超参数优化中涉及的大部分步骤将在后台进行处理。这种方法极大地改变了在训练机器学习模型中涉及的传统工作流。
AutoML完全改变了整个机器学习领域的游戏规则,因为对于许多应用程序,不需要专业技能和知识。许多公司只需要深度网络来完成更简单的任务,例如图像分类。那么他们并不需要雇用一些人工智能专家,他们只需要能够数据组织好,然后交由AutoML来完成即可。
3.4 参考文献
[1] Samuel A L. Some Studies in Machine Learning Using the Game of Checkers. Ⅱ-Recent Progress [M]//LEVY D. Computer games I. New York: Springer, 1988: 366-400.
[2] 李航.统计学习方法[M].北京:清华大学出版社,2012.
[3] 周志华.机器学习[M].北京:清华大学出版社,2016.
[4] 周志华.机器学习与数据挖掘[J].中国计算机学会通讯,2007, 3(12): 35-44.
[5] 阿培丁.机器学习导论[M].范明,昝红英,牛常勇,译.北京:机械工业出版社,2009.
[6] ALPAYDIN E. Introduction to machine learning[M]. 3th ed. Cambridge, MA:MIT Press, 2014.
[7] BISHOP C M. Pattern recognition and machine learning[M]. New York: Springer, 2006.
[8] CARBONELL J G. Machine learning: paradigms and methods[M]. Amsterdam: Elsevier North-Holland, 1990.
[9] DIETTERICH T G. Machine-learning research[J]. AI magazine, 1997, 18(4): 97-97.
[10] RUMELHART D E, HINTON G E, WILLIAMS R J. Learning representations by back-propagating errors[J]. Cognitive modeling, 1988, 5(3): 1.
[11] COVER T M, HART P E. Nearest neighbor pattern classification[J]. IEEE transactions on information theory, 1967, 13(1): 21-27.
[12] DALAL N, TRIGGS B. Histograms of oriented gradients for human detection[C]//IEEE Computer Society. Proceedings of the 2005 IEEEconference on computer vision andpattern recognition. Washington, DC:IEEE Computer Society, 2005, 1: 886-893.
[13] KAZEMI V, SULLIVAN J. One millisecond face alignment with an ensemble of regression trees[C]//IEEE Computer Society. Proceedings of the 2014 IEEE conference on computer vision and pattern recognition. Washington, DC:IEEE Computer Society, 2014: 1867-1874.
[14] HAND D J, TILL R J. A simple generalisation of the area under the ROC curve for multiple class classification problems[J]. Machine learning, 2001, 45(2): 171-186.
