大数据探索及预处理
现在几乎人人都在谈论大数据和人工智能,然而应用大数据和人工智能技术的基本前提是数据。不论数据的拥有方还是数据分析解决方案及工具的提供方,其终极目标都是“通过数据分析,从数据中找出洞见并应用于实际场景中带来价值”。
数据探索、数据预处理等工作是进行数据分析的首要工作。不论是采用大数据的工具还是采用相对较小的数据集上的数据挖掘的工具,模型的构建都需要经过对数据不断地探索、选择和加工合适的字段、采用合适的算法并训练模型等过程。
数据探索的目的是了解数据的状态,数据预处理则是为了将数据加工为更有价值的形态。数据分析者应当具有很好的意识,能够感知数据的价值,具备数据加工能力。
2.1大数据探索
大多数情况下,数据分析的过程必须包括数据探索的过程。数据探索可以有两个层面的理解:一是仅利用一些工具,对数据的特征进行查看;二是根据数据特征,感知数据价值,以决定是否需要对别的字段进行探索,或者决定如何加工这些字段以发挥数据分析的价值。字段的选取既需要技术手段的支撑,也需要数据分析者的经验和对解决问题的深入理解。
2.1.1数值类型
在进行数据分析时,往往需要明确每个字段的数据类型。数据类型代表了数据的业务含义,分为3个类型:
(1)区间型数据(Interval)
数值型数据的取值都是数值类型,其大小代表了对象的状态。比如,年收入的取值,其大小代表了其收入状态。
(2)分类型数据(Categorical)
分类型数据的每一个取值都代表了一个类别,如性别,两个取值代表了两个群体。
(3)序数型数据(Ordinal)
和分类型数据非常相似,每个取值代表了不同的类别。但是,序数型的数据还有另外一层含义就是每个取值是有大小之分的。比如,如果将年收入划分为3个档次:高、中、低,则不同的取值既有类别之分,也有大小之分。
如果不了解字段的实际业务含义,数据分析人员可能会出现数据类型判断失误。比如字段的取值为“1”“2”“3”等,并不意味着是一个数值类型,它的业务含义还可以是一个分类型的字段,“1”“2”“3”分别代表了一个类别,其大小没有任何含义。所以,充分了解字段的含义是很重要的。
很多的数据分析工具会根据数据中的字段的实际取值,做出类型的自动判断:如字符型的数据,一般都认定为分类型数据;如某个字段的所有取值只有“1”“2”“3”,则判断其为分类型变量,然后经过用户的再次判断,其很可能是序数型变量。
不同的数据类型,在算法进行模型训练时,处理和对待的方式是不同的。区间型数据是直接进行计算的;分类型数据是先将其转换为稀疏矩阵:每一个类别是一个新的字段,然后根据其取值“1”“0”进行计算。
在很多场景下,人们习惯将分类型数据和序数型数据统称为分类型数据,即数据类型可以是两个:数值型数据(区间型数据)和分类型数据(分类型数据和序数型数据)。
2.1.2连续型数据的探索
连续型数据的探索,其关注点主要是通过统计指标来反映其分布和特点。典型的统计指标有以下几个:
(1)缺失值
取值为空的值即为缺失值。缺失值比例是确定该字段是否可用的重要指标。一般情况下,如果缺失率超过50%,则该字段就完全不可用。
在很多情况下,我们需要区别对待null和0的关系。Null为缺失值,0是有效值。这个区别很重要,要小心区别对待。例如,某客户在银行内的某账户余额为null,意味着该客户可能没有该账户。但是如果将null改为0,则是说用户有该账户,且账户余额为零。
(2)均值(Mean)
顾名思义,均值即平均值。其大小反映了整体的水平。一个数学平均成绩是95分的班级,肯定比平均成绩是80分的班级的数学能力要好。
(3)最大值和最小值
最大值和最小值即每个数据集中的最大数和最小数。
(4)方差
方差反映各个取值距平均值的离散程度。虽然有时两组数据的平均值大小可能是相同的,但是各个观察量的离散程度却很少能相同。方差取值越大,说明离散程度越大。比如,平均成绩是80分的班级,其方差很小,说明这个班级的数学能力比较平均:没有多少过高的成绩,也没有多少过低的成绩。
(5)标准差
标准差是方差的开方,其含义与方差类似。
(6)中位数(Median)
中位数是将排序后的数据集分为两个数据集,这两个数据集分别是取值高的数据集和取值低的数据集。比如,数据集{3,4,5,7,8}的中位数是5,在5之下和5之上分别是取值低和取值高的数据集。数据集{2,4,5,7}的中位数应当是(4 + 5)/2=4.5。
(7)众数(Mode)
众数是数据集中出现频率最高的数据。众数最常用的场景是分类型数据的统计,但是其也反映了数值型数据的“明显集中趋势点的数值”。
均值、中位数、众数的计算方式各有不同,如表2-1所示。
表2-1 均值、中位数、众数的例子

(8)四分位数(Quartile)
四分位数,即用三个序号将已经排序过的数据等分为四份,如表2-2所示。
表2-2 四分位的例子

第二四分位数(Q2)的取值和中位数的取值是相同的。
(9)四分位距(Interquartile Range,IQR)
四分位距通过第三四分位数和第一四分位数的差值来计算,即IQR=Q3-Q1。针对上表,其IQR=61-34=27。四分位距是进行离群值判别的一个重要统计指标。一般情况下,极端值都在Q1-1.5×IQR之下,或者Q3 + 1.5×IQR之上。著名的箱形图就是借助四分位数和四分位距的概念来画的,如图2-1所示。
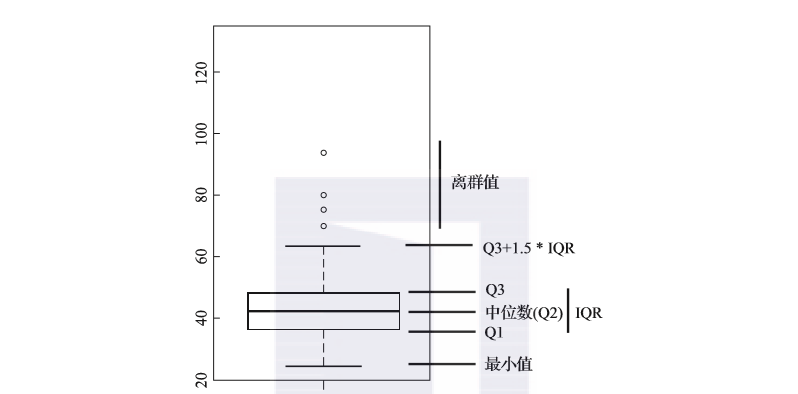
图2-1 箱形图及IQR
箱形图中的上下两条横线,有可能是离群值分界点(Q3 + 1.5×IQR或Q1-1.5×IQR),也有可能是最大值或最小值。这完全取决于最大值和最小值是否在分界点之内。
(10)偏斜度(Skewness)
偏斜度是关于表现数据分布的对称性的指标。如果其值是0,则代表一个对称性的分布;若其值是正值,代表分布的峰值偏左;若其值是负值,代表分布的峰值偏右。在图2-2中给出了偏斜度的示例。
图2-2 Skewness的含义
Skewness的绝对值(不论是正值还是负值)如果大于1是个很明显的信号,你的数据分布有明显的不对称性。很多数据分析的算法都是基于数据的分布是类似于正态分布的钟型分布,并且数据都是在均值的周围分布。如果Skewness的绝对值过大,则是另一个信号:你要小心地使用那些算法!
不同的偏斜度下,均值、中位数、众数的取值是有很大不同的:
由图2-3可见,在数据取值范围相同的情况下,中位数是相同的。但是均值和众数却有很大的不同。所以,除了偏斜度指标可以直接反映分布特征外,还可以用表2-3中的方法来判断。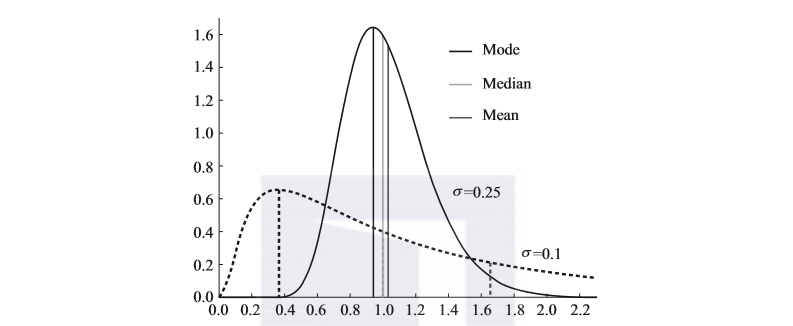
图2-3 众数、均值及中位数在不同分布下的比较
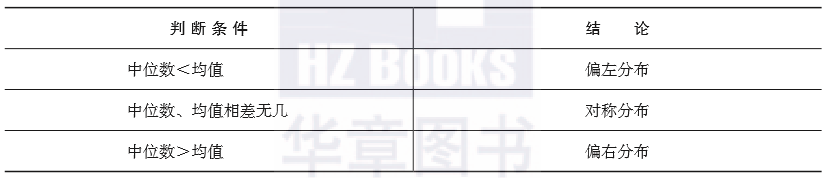
表2-3 通过中位数和均值的差异来判断分布的偏斜情况
(11)峰态(Kurtosis)
标准正态分布的峰态的值是3,但是在很多数据分析工具中对峰态值减去3,使得:0代表是正态分布;正值代表数据分布有个尖尖的峰值,高于正态分布的峰值;负值代表数据有个平缓的峰值,且低于正态分布的峰值。
峰态指标的主要作用是体现数值分布的尾巴厚度,尖峰对应着厚尾,即Kurtosis大于0时,意味着有一个厚尾巴。尖峰厚尾也就是说,在峰值附近取值较集中,但在非峰值附近取值较分散。图2-4所示为一个峰态的例子。
在连续型数据的探索中,需要重点关注的指标首先是缺失率,然后是均值、中位数等指标,这些指标能帮助数据分析者对数据的特征有很好的了解。偏斜度是另外一个非常重要的指标,但其绝对值接近1或大于1时,必须对其进行log转换才能使用,否则该指标的价值将大打折扣。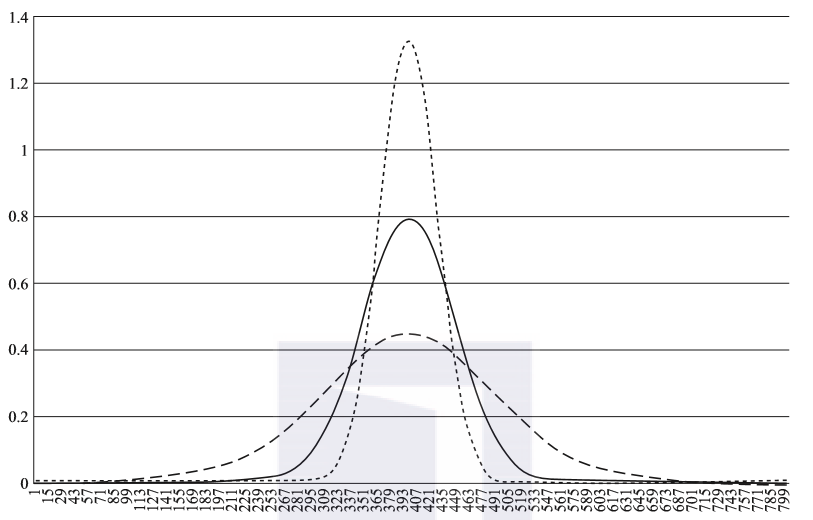
图2-4 峰态的例子
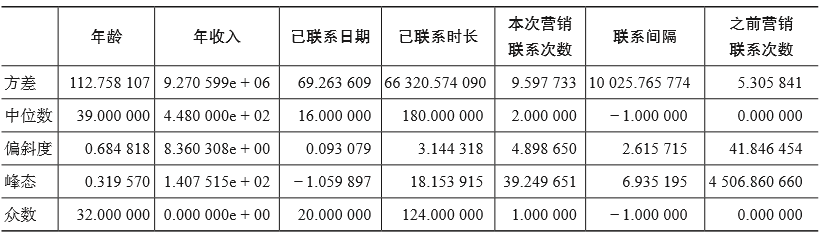
Python Pandas中DataFrame的describe方法默认只统计连续性字段的最大值、最小值、均值、标准差、四分位数,如果想获取其他的特征值,需要调用相应的函数来获得。下面是一段示例代码,其运行结果通过表2-4来展示。
表2-4 连续型变量数据探索示例代码的运行结果
2.1.3分类型数据的探索
分类型数据的探索主要是从分类的分布等方面进行考察。常见的统计指标有以下几个:
(1)缺失值
缺失值永远是需要关心的指标,不论是连续型数据,还是分类型数据。过多的缺失值,会使得指标失去意义。
(2)类别个数
依据分类型数据中类别的个数,可以对指标是否可用有一个大致的判断。例如,从业务角度来看,某指标应当有6个类别,但实际样本中只出现了5个类别,则需要重新考虑样本的质量。再如,某个分类型变量只有一个类别时,对数据分析是完全不可用的。
(3)类别中个体数量
在大多数情况下,如果某些类别中个体数量太少,如只有1%的比例,可以认为该类别是个离群值。关于分类型变量离群值的研究比较多,但是如果脱离业务来谈分类型变量的离群值,是不妥当的。不平衡数据就是一个典型的与业务有关的例子。比如,从业务角度来看,购买黄金的客户只占银行全量客户的很小的一个部分,如果采取简单随机抽样的方式,“是否购买”列的值将只有极少的“是”的取值。但是,不能将“是”直接判断为离群值,反而“是”有极其重要的业务含义。所以,数据分析者需要灵活地认识和对待类别中个体数量的问题。
(4)众数
和连续型数据的含义一样,众数是数据集中出现频率最高的数据。比如,针对某个分类型取值A、B、C、D中C的出现次数最多,则C就是众数。
以下是一段分类型变量数据探索示例代码,其运行结果通过表2-5来展示。
表2-5 分类型变量数据探索示例代码的运行结果
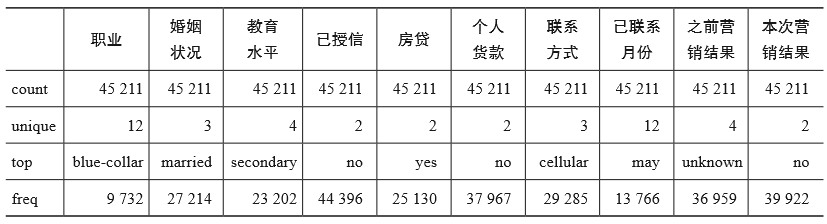
应用Python Pandas的相关函数能够非常容易得到分类型变量的探索结果,表2-5所示就是数据探索示例代码的运行结果。
2.1.4示例:数据探索
我们采用加州大学欧文学院创建的Machine Learning Repository 网站上的一个数据集,Bank Marketing Data Set 。Machine Learning Repository是一个非常著名的网站,里面的数据集最早被分享于1987年。很多著名的计算机类的论文都引用这个网站上的数据。Bank Marketing Data Set来自葡萄牙某银行的市场营销数据,表2-6展示了部分字段的类型及取值范围。
表2-6 Bank Marketing Data Set的字段说明
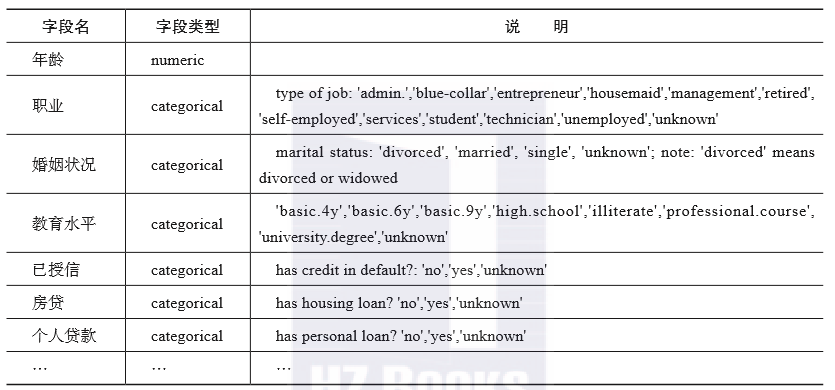
该案例所描述的场景是葡萄牙某银行机构的电话营销活动,通过调查客户的基本信息来预测客户是否会认购定期存款,所调查的客户信息包括年龄、工作类型、婚姻状况、教育、是否有个人贷款等。在本节中,我们使用bank-full数据集完成一个数据探索示例,包括单个变量的分布情况、双变量之间的关系,这些探索可以为缺失值处理、异常值和离群值处理、特征变换做一个很好的铺垫。
通过可视化工具可以展现单变量的分布特征。对于连续型变量age、balance、duration,通过折线图和箱形图展现数据的情况。对于分类型变量job、marital、education、y,通过柱状图展现数据的情况。


上述代码是绘制age、balance、duration变量的折线图,并将其在一个图中集中展现。通过观察折线图可以初步掌握数据的缺失情况、异常情况和离群值情况等。比如balance变量存在一些极大值情况,但大多数值都落在小区间范围内。图2-5所示是三个变量age、balance、duration的折线图结果。
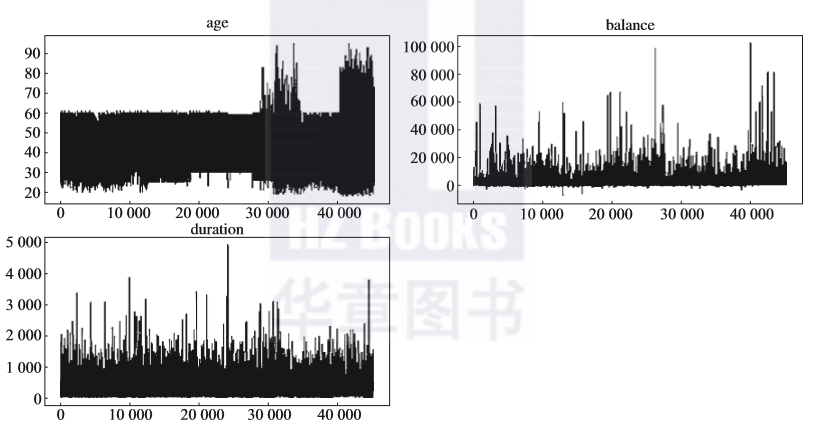
图2-5 折线图的示例
箱形图从分位数的角度来展现变量的分布特征,人们往往会根据箱形图做出离群值的过滤条件等数据清洗规则。

从图2-6中可以看出,age变量取值范围比较大,离群点较少;balance变量和duration变量的取值范围比较小,都分布在小值范围内,离群点分布范围比较广。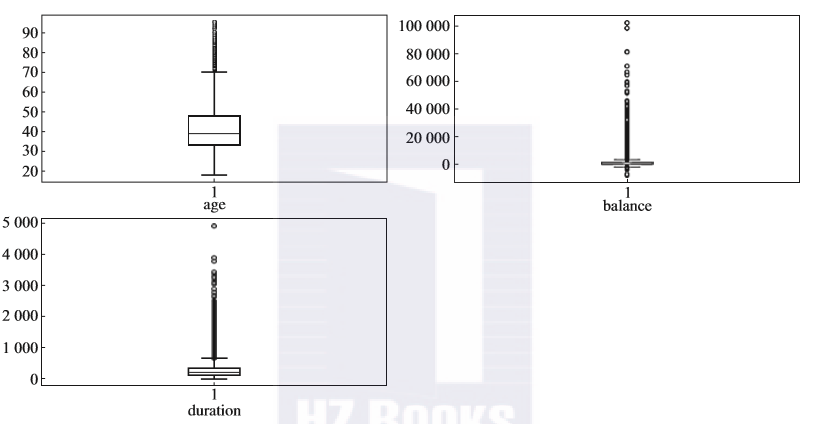
图2-6 箱形图的示例
分类型变量一般首先通过柱状图来展现分布特征。下面的代码是分别绘制数据集中变量job、marital、education、y的柱状图。为了展现更为详尽的柱状图的绘制原理,我们采用“统计各分类值取值个数,然后再绘制柱状图”的方法。
从图2-7的4个柱状图中可以看出每个变量的取值分布,比如job变量类别比较多,其中一个类别取值比较少;education变量中unknown的值个数比较少;y变量的数据分布不均衡。数据集出现预测变量类不均衡的情况,在构建分类型预测模型时一般需要将数据处理为均衡数据集才可使用。读者可以参考5.5.2节中的介绍以了解处理的方法和过程。
双变量的关系探查往往能发现非常有价值的数据洞见。双变量探查包括连续型-连续型、连续型-分类型、分类型-分类型这些关系,连续型-连续型使用散点图来探查它们的线性关系,分类型-分类型使用堆叠柱状图或卡方检验,连续型-分类型使用ANOVA方差进行分析。本案例通过连续型-连续型进行举例说明,选择使用age变量和balance变量。
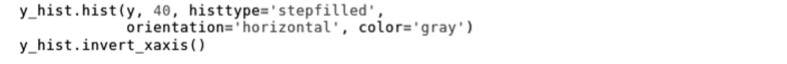
上述代码通过散点图和两个直方图(如图2-8所示)可以从变量分布以及变量间的关系的角度发现有价值的结论。例如,对于age的不同取值,balance的取值都集中在20000的范围内,20000之外的取值比较少;财富在20000以上的人群年龄基本在40岁以上;60岁是一个明显的财富分割点,即60岁以上仍然拥有20000以上财富的人数陡降。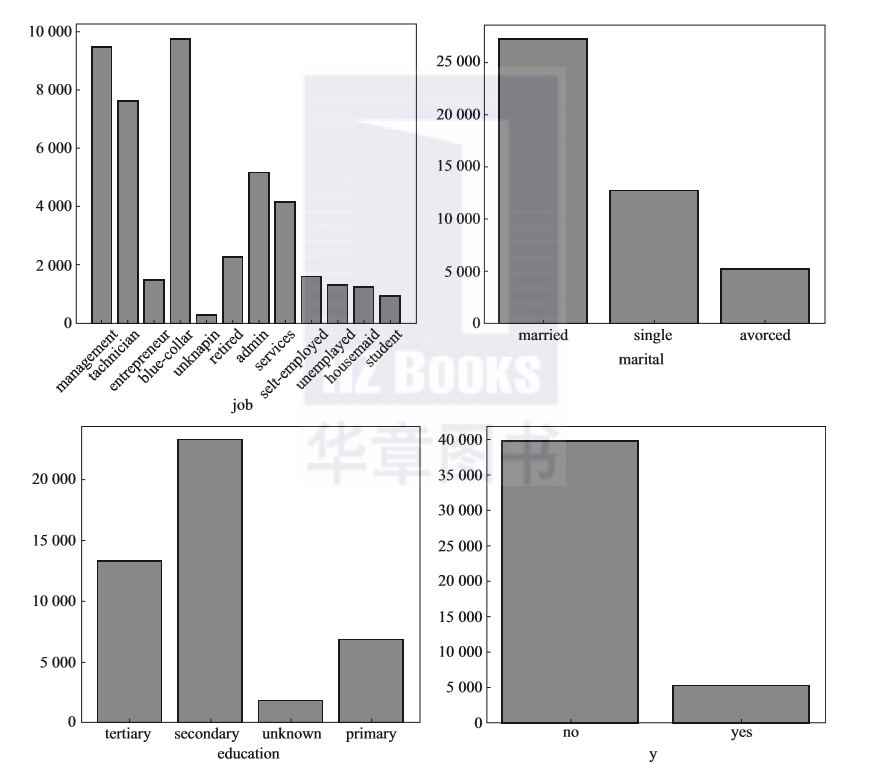
图2-7 柱状图示例
图2-8只是从分布的角度来看是否能发现有意义的业务洞察。若单纯计算两个变量间的相关性并进行展示,则可以参考下面的例子。
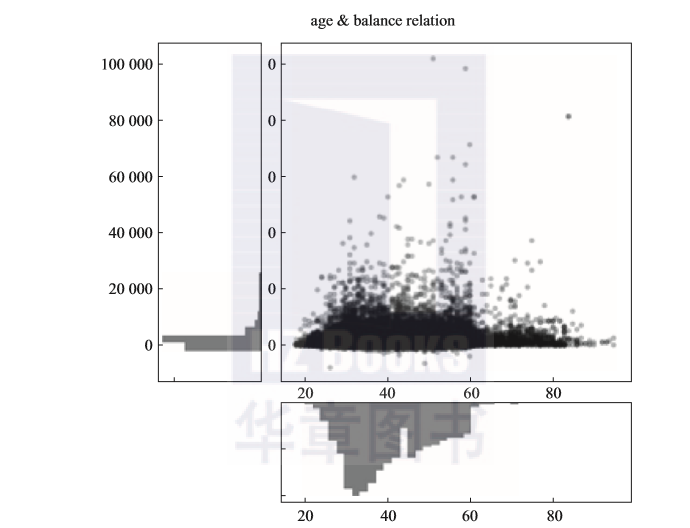
图2-8 双变量关系探索的示例(X轴是age变量,Y轴是balance变量)
从图2-9中可以看出,age和balance之间的相关性只有0.098,说明它们之间的相关性比较弱。计算变量间的相关系数,可以为后期进行模型构建、变量选择、衍生指标加工提供依据。在1.4节中,我们鼓励数据分析者能够输出两种价值,其实图2-8及其对应的解读就是一个很好的示例。
在数据分析实践中,笔者强烈建议数据分析者能够花费大量的时间在数据探索的工作上。这样既能保证数据分析者对业务的深刻理解,也能为后续的数据预处理奠定非常好的基础。
图2-9 双变量相关矩阵的示例
2.2数据预处理
数据的重要性在大多数情况下都超过了算法的重要性。数据预处理是数据分析过程中的一个重要步骤。多年以来,人们在数据质量上的持续投入大幅减少了越界、缺失、不一致等问题。但是,数据质量问题仍然存在。数据分析者应当对数据质量时刻保持警惕,因为质量很差的数据是很难得到有用的分析结果的。既然数据质量问题不可避免,那么处理它们是数据预处理的工作之一。数据预处理的完整工作应当包括数据清洗、数据集成、数据变换和数据归约处理。
2.2.1数据清洗
数据清洗就是发现和改正(或移除)不准确或不精确的数据。数据仓库的数据治理模块重点关注数据质量问题,并拥有完善的数据清洗功能。本书讨论的数据清洗的工作,在数据仓库的管理者看来,是属于他们的工作范畴。但是,我们并不认为,从数据仓库中出来的数据都是没有问题,况且数据分析的数据源并不只有数据库或者数据仓库。在数据分析领域,常用的数据清洗包括以下几种:
1. 缺失值的处理
处理缺失值是最为常见的数据清洗工作。在数据分析中会遵从一些规则来填补缺失值。比如:
- 对于连续型变量,采用均值来代替缺失值;
- 对于序数型分类型变量,采用中位数来代替缺失值;
- 对于分类型变量,采用众数来代替缺失值。
2. 越界值的处理
少数的越界值会被当作离群值来处理;大量的越界值需要通过业务知识来判断。比如,对于银行客户的资产负债比,如果有较多人是负数,就需要高度怀疑数据的加工方式出现了问题。因为从业务角度来看,这种情况不可能是普遍现象。
Python提供了很多方法来处理缺失值。最简单的方法是调用replace函数或者直接调用DataFrame中的fillna函数进行缺失值的替换。
上述代码用来填充空白值,其运行结果如图2-10所示。
图2-10 数据空白值填充的示例
对于越界值的处理会更复杂,因为需要用不同的业务知识来判断越界值产生的原因,然后再决定越界值的处理方式:是简单地将越界值移除,还是对越界值进行纠正?但这些操作的前提是先识别越界值。对于连续型的变量,可以采用Z-score将数据变换成均值为0、标准差为1的数据,然后Z-score的值超过3~-3的数据都会被认为是越界值,并将这些值从数据中去除。
从上述代码的处理结果中可以看出,有5002(初始数据有45211行,过滤离群值后有40209行)行包含离群值的数据被过滤掉。类似于拼写错误、值与字段含义不匹配等数据清洗的工作,一般都需要借助一些批处理的脚本来处理。
在一些数据预处理工具中,针对一些情况,其会自动做一些处理,比如:
- 如果一个变量的缺失值比例大于设定阈值(默认是50%),那么该变量将被忽略;
- 对于连续型变量,如果该变量的最大值等于最小值(即为常量),那么该变量将被忽略;
- 对于分类型变量,如果该变量的众数在记录中所占比例大于设定阈值(默认是95%),那么该变量将被忽略。

在上面的例子中,第一个条件使用isnull()函数标记数据中全部的缺失值,再通过mean()函数计算缺失值所占的比例,最后判断是否大于设定的阈值;第二个条件判断数据的每一个值是否都相同(是否是常量);第3个条件通过value_counts()函数和max()函数计算数据中每一个变量众数的比例,并判断是否大于设定的阈值。我们只要通过这样一条语句就可以完成上述所有的数据预处理过程。经过这些条件的处理,数据变成了16个变量,说明其中一个变量因为满足这些条件而被忽略了。下面我们单独执行每一个条件,看看是什么条件被触发了。
在图2-11中,分别执行数据预处理的3个条件,我们看到“已授信”字段触发了“众数比例大于95%”这个条件而被忽略。基于这个原因,初始数据集从17个字段变成了最终的16个字段。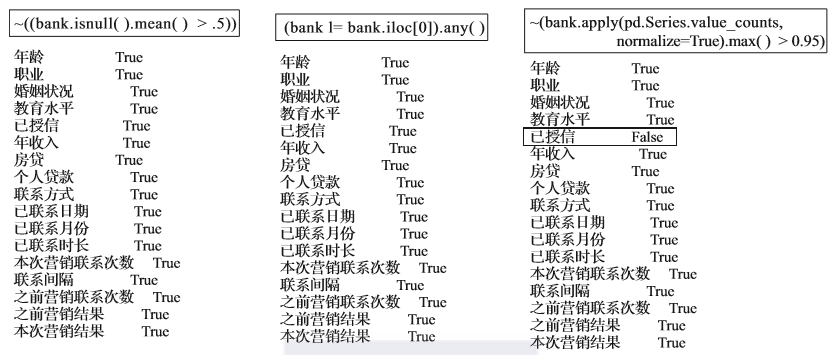
图2-11 分别执行数据预处理的3个条件,查看触发条件
2.2.2数据变换
对于连续型变量,如果该变量的取值的个数小于设定阈值(默认是5),那么将该变量转化为有序型分类变量。对于有序型分类变量(数值类型),如果该变量的类型的个数大于设定阈值(默认是10),那么将该变量转化为连续型变量。
1. 连续型变量的变换
对于连续型变量,为了保证数据中不同的字段保持同样的尺度(这样既可以防止某些字段在建模过程中发生溢出,又可以保证每一个字段在模型中的权重相同),我们需要进行一些尺度变换的操作。分箱(binning,又称离散化)是将连续型数据转换为分类型变量,转换的目的是提高变量的解释性。
(1)尺度变化
为了使数据尺度一致,可以对原始数据进行中心化、标准化、归一化、Z-score变换、最小-最大值变换等。在表2-7中我们列举了典型的数据转换方法。
(2)分箱变换
对于一些连续型变量,从业务和数据特点上考虑,需要将连续型数据变为分类型数据,可以进行binning操作,常用的分箱变换方法如表2-8所示。
分箱技术的方法有很多种,比较常用的有下面的3种方式:
- 等宽度间隔(Equal Width Intervals);
- 基于已扫描个案的等百分位(Equal Percentiles Based on Scanned Cases);
- 基于已扫描个案的平均值和选定标准差处的分割点(Cutpoints at Mean and Selected Standard Deviations Based on Scanned Cases)。
表2-7 典型的数据转化方法

表2-8 分箱变换方法

从中位数直接将连续型数值划分为两个分组是比较常见的等宽度间隔的分箱做法。在偏峰的情况下,是可以划分出明显的高低两个分组的,如图2-12所示。
图2-12 采用中位数对连续型变量进行划分
在没有具体业务要求的情况下,上述三种方式都是合适的。但是我们在一个关于银行的实际案例中,遇到这样的一种情况:当对某个连续值进行分箱时,遇到的问题不仅仅是等宽或者等值的问题,真正的问题是怎么样的分箱对业务具有指导意义。不同的分箱,每个值的背后都是一批客户,而在银行的营销力量有限的情况下,必然需要对不同的群体采取不同的策略。最为简单的策略就是,对高价值的客户采用费用较高但是可能带来高回报的营销活动,而对低价值的客户,则可以采用费用较低的营销。并且往往低价值的客户是占多数的,其分布大多如图2-13所示: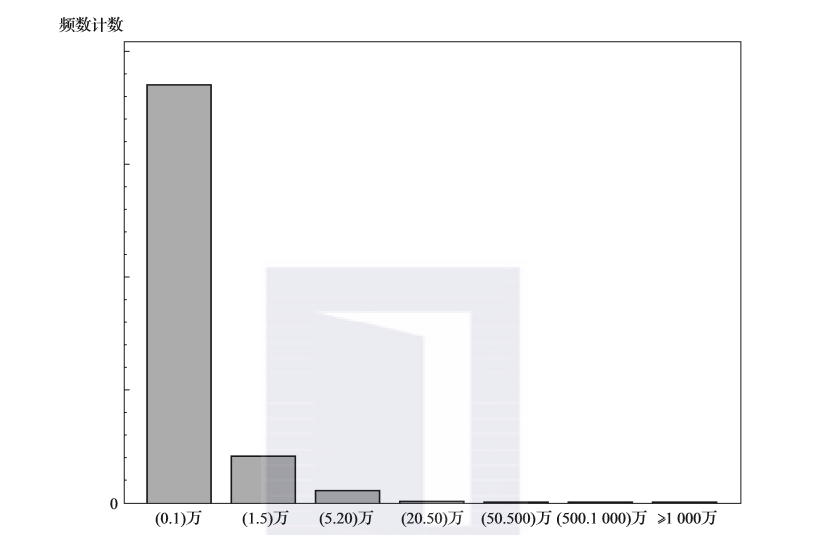
图2-13 很多情况下,低价值的客户总是占多数
针对如图2-13所示的分布,等宽分布、等值分布都比较难以确定“什么样的阈值可以区分高价值客户、低价值客户”。所以,我们采用了经典的“80%~20%”的方法,即80%的客户可能会贡献较少的价值,而20%的人往往会贡献较多的价值。图2-14代表了一种典型的分箱策略。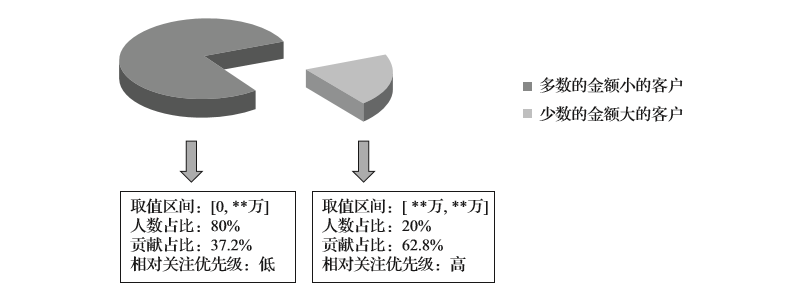
图2-14 按照80%-20%的划分能够将高价值的客户显著区分出来
我们采用2.1.4节中的数据集来展现分箱的实例。在银行的营销活动中,营销产品的设计往往关注客户的年龄。不考虑客户的职业等其他的特征,一般青壮年客户有成家立业的金融需求,中老年的客户则倾向于投资、存款等。所以,年龄阶段的划分(分箱)可以作为一个衍生字段。
为此,我们用SciKit-learn中的KBinsDiscretizer来生成衍生字段。KBinsDiscretizer提供了3种分箱策略:
- uniform:每一个分箱都有相同的宽度;
- quantile:每一个分箱都有相同的数据个数;
- kmeans:分箱中的每个值都具有与kmeans聚类相同的最近中心。
利用KBinsDiscretizer对2.1.4节中的数据进行年龄变量的分箱操作,使用上述3种分箱策略生成3个衍生字段:“年龄分箱_uniform”“年龄分箱_quantile”和“年龄分箱_kmeans”,分箱时选择的分箱数是6,然后对原始变量“年龄”,以及3个衍生字段再次进行数据探查,查看数据分布的变化。
上述代码生成3个分箱的结果,通过查看前5行数据(如表2-9所示)可以看出3个分箱的决策是各不相同的,如年龄58,按照uniform策略,则属于编号是“3.0”的分箱区间;按照quantile策略,则属于编号是“5.0”的分箱区间;按照kmeans策略,则属于编号是“3.0”的分箱区间。
表2-9 3种分箱策略的结果示例
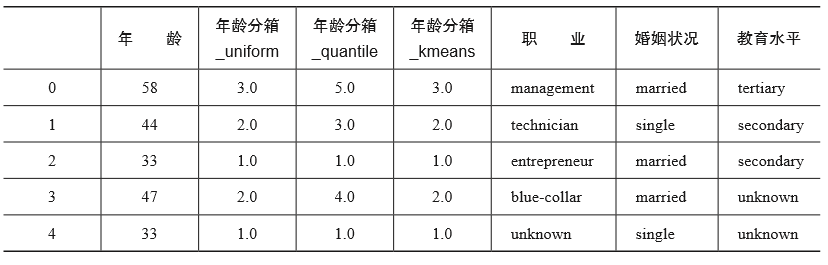
我们还可以通过查看分箱前后的柱状图来观察和理解各个分箱结果的不同。图2-15所示是源数据的分布以及3种分箱策略的结果展示。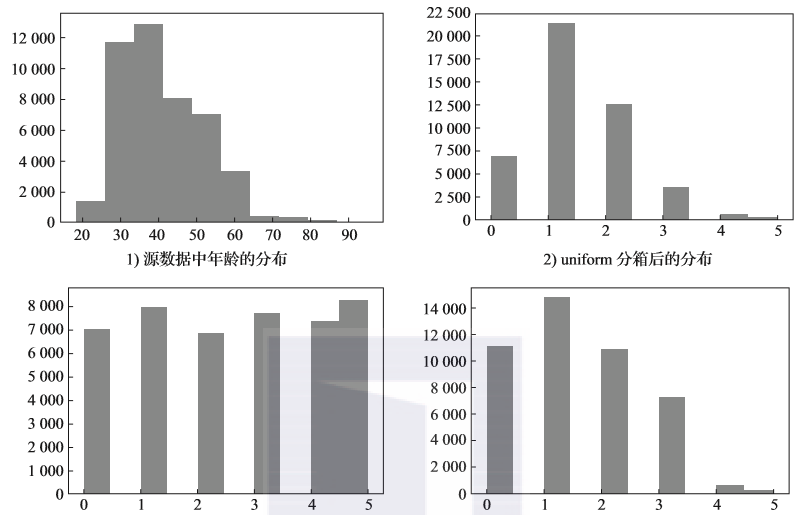
图2-15 源数据分布及3种分箱策略的结果示例
从年龄变量的分布来看,该银行的客户主要是30岁到40岁的青壮年,小于30岁的客户很少,而年龄超过60岁的客户更少,这个结果间接印证了前面所进行的数据探索的结果——60岁是一个财富的分割点。使用uniform分箱策略生成的衍生字段因为每个分箱的宽度相同,因此基本上保留了年龄变量的分布特征。
而使用quantile分箱策略生成的衍生字段却完全改变了数据分布的情况。因为这个分箱策略是使每一个分箱中包含数量基本相同的数据,所以其分布得也非常均匀。我们通过KBinsDiscretizer的bin_edges_方法查看使用quantile分箱策略进行的分箱操作,其分箱边界为18~31、31~35、35~39、39~45、45~52和52~95。其在年龄分布非常集中的区间,分箱非常密集。其中31~45岁这个区间就包含了3个分箱。
使用kmeans分箱策略相当于对年龄变量进行了6个聚类的kmeans聚类操作。因为是基于kmeans算法,取值更接近的数据会被划分在一个聚类里,所以kmeans分箱策略也基本上保留了年龄变量的分布特征,其分箱边界也基本上接近于uniform的分箱边界。
2. 分类型变量的变换
在很多的机器学习的算法实现中,在调用算法之前,会首先对分类型数据做一些变换。这些变换会提高模型的稳定性。比较常见的变换如表2-10所示:
表2-10 分类型变量的变换

对于分类型变量,为了在模型中体现出分类型变量自身的特点,比如每个类型只是一个标记,无大小之说,每个类型都可以作为一个独立的参数参与模型构建,这样可以对分类型变量做数值编码,变换为虚拟dummy变量或者成为标记indicator变量。
对于某些分类型变量,其类型是名义nominal变量,为了提高模型的稳定性,需要对分类型变量的各个类型按照其数据量的多少重新排序。这样原来的类型标记被重新编码和排序。对于某些数据集,其含有一系列相关的多个分类型字段,各个字段存在业务逻辑上的关系,并且各个字段的取值也存在关联。这样,我们就可以将这些字段合并为一个字段。这样做既可以减少模型的维度和复杂度,也可以消除各个自变量之间的相关性,保持彼此的独立性,提高模型的质量。
(1)类别的数值编码
当训练模型时,数据集中的字段包含符号字段(或者称为分类字段)时,而且该字段也需要被用来参与建模,并且该模型算法需要使用所有记录的数值来进行算法计算。这种情况下就对符号字段提出了挑战,那么如何用数值来表示该符号字段的各个分类呢?
一般的做法是将该符号字段编码为一组数值字段,该组数值字段的个数等于该符号字段的分类个数,一个分类对应一个数值字段。对于该符号字段的每一个取值,对应于该值的那个数值字段的值均被设置为1,其他数值字段的值均被设置为0。这组数值字段(或者称为衍生字段)被称为indicator(指示)字段,或者dummy(虚拟)字段。
如表2-11所示,对于下列3条数据,X是一个符号字段,取值为A、B、C,那么它可以被转化为衍生字段X1、X2、X3。
表2-11 分类型变量的变换为dummy字段

从表2-11中可以看出,符号字段的分类A被编码为(1 0 0),B被编码为(0 1 0),C被编码为(0 0 1)。
按照此方式编码后,这些符号字段被转换为一系列取值为0和1的稀疏矩阵。在建模的计算过程中,所要估计的模型参数的个数就会增加,但在实际的运算中,只有取值为1的变量需要参与计算,其他取值为0的变量可以忽略,这样可以极大地节省内存空间并提高计算效率。当模型参数被估计出来后,建模过程完成时,我们可以从模型结果中得到该字符变量的各个分类变量对应的模型参数和重要性。
在算法的具体计算过程中,经常会用到“类别的数值编码”的方式,将类别型的字段转换为dummy字段。下面的例子就说明了这个过程。
我们采用一个员工个人信息的数据集,包括字段:id(员工编号),gender(性别),bdate(出生日期),educ(教育程度),jobcat(工作类别),salary(工资),salbegin(起始工资),jobtime(工作时间),prevexp(先前经验),minority(民族)。该数据集如表2-12所示。
表2-12 员工个人信息的示例
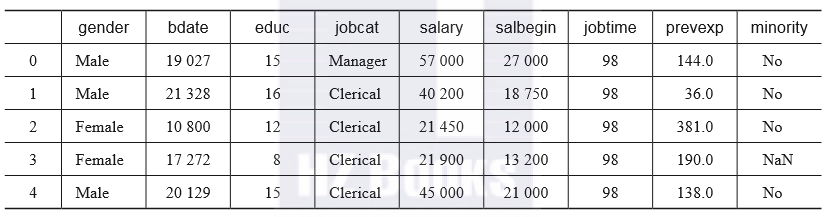
我们根据educ,jobcat,salary,salbegin字段来预测gender字段,此处选取Binomial Logistic Regression二项逻辑回归模型,使用GLM模型来完成。虽然该模型并不具有实际意义,但是可以说明符号型字段在建立模型中起到的作用。
educ为取值8、12、14、15、16、17、18、19、20、21的数值型分类变量,但其是有顺序的,被称为ordinal有序分类变量;jobcat为取值Clerical、Custodial和Manager的三值字符型分类变量,是无顺序的,被称为nomial名义分类变量;salary和salbegin为连续型变量;gender为取值f和m的二值字符型分类变量,被称为flag标记变量或者nomial名义分类变量。对于建立的模型来说,educ、jobcat、salary、salbegin作为预测变量,gender作为目标变量。一般在回归模型中,educ和jobcat被称为factor因子变量,salary和salbegin被称为covariates协变量。
我们采用Python 类库StatsModels建立二项回归模型。由于educ的值是数字,所以需要使用C操作符定义其为分类型变量 ;因为jobcat的值是文字,模型会自动识别其为分类型变量。通过使用StatsModels建立模型,所使用的相关Python脚本如下:
上述代码运行得到的结果如下: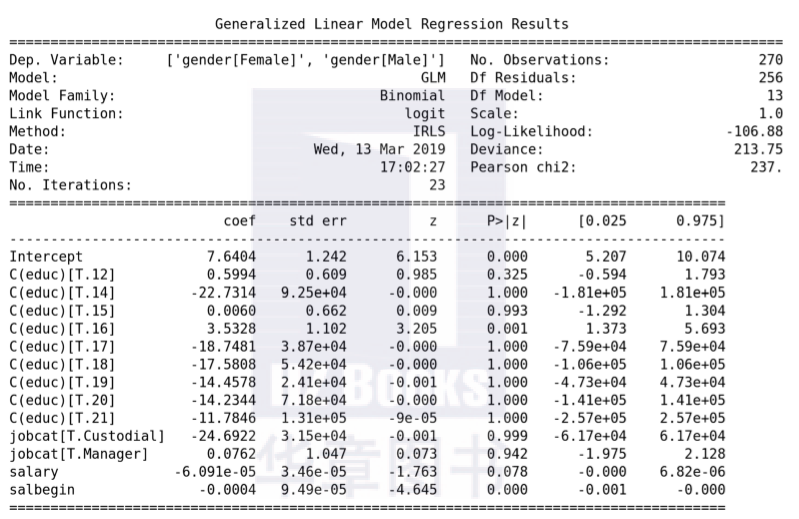
从结果中的Coefficients的个数可以看出,educ和jobcat分类型变量被转化成了dummy虚拟变量,分别只显示了分类个数减1个系数,说明未被显示的那一个系数成了冗余。对于分类型字段来说,一般其中的一个分类都会被设置为冗余,这个特性在其他的机器学习模型算法中都适用。我们用jobcat作为例子,其包含Custodial、Manager和Clerical,使用两个虚拟变量jobcat[T.Custodial]和jobcat[T.Manager]来表示这3个可能的取值。如果jobcat[T.Custodial]等于1,表示jobcat的取值是Custodial;如果jobcat[T. Manager]等于1,表示jobcat的取值是Manager;如果jobcat[T.Custodial]和jobcat[T. Manager]都不等于1,表示jobcat既不是Custodial,又不是Manager,则jobcat为Clerical。进而从P-value显著性指标可以看出salbegin对gender的影响最大,起决定性作用,说明起始工资对性别的影响最大。
利用残差分析来验证该模型是否适合该数据。因为残差等于变量真实值和预测值的差,线性模型越准确,残差的分布就越接近于0,所以通过残差分析来观察残差的分布是否主要分散在0的周围,就可以判断该线性模型是否适合该数据。
从图2-16所示的残差的分布来看,残差点比较均匀地分布在水平带状区域中,大多数点集中在0点,0点两边的点分布比较分散,说明这个线性回归模型比较适合该数据。
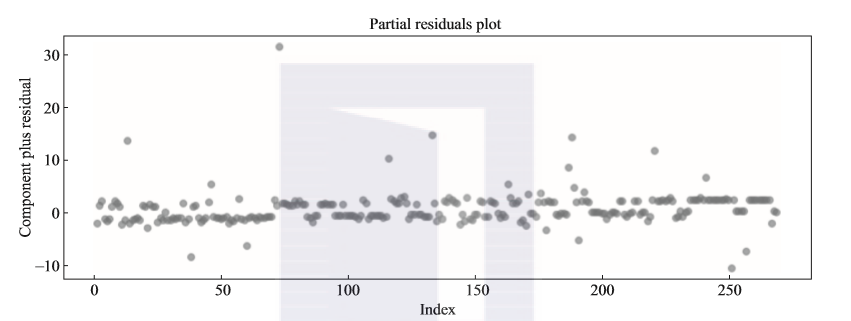
图2-16 模型的残差分布
(2)关联字段的合并
稀疏矩阵是数据分析时一种常见的数据形式。所谓稀疏矩阵是指一个矩阵(二维或多维)中,非零元素的值占很小的一部分,绝大多数元素取值为零,并且非零元素的分布一般没有什么规律。笔者在做一个实际的项目时,遇到一个稀疏矩阵的问题:二维表中的每一列代表客户持有的产品状态,1代表持有,0代表未持有。要找出客户持有产品的规律,就是将稀疏矩阵中每行的取值转化为一个字符串,即字符串“0000000000”代表十列数据取值都为零的情况。通过这种方式,其实是用新的一列代表了原来10列的数据信息,可以很方便地看出客户持有产品的状态。图2-17所示就是一个典型的例子。
3. 分布变换
在大多数模型中,都要求因变量服从和接近正态分布,正态分布是统计建模的基石,是许多模型的理论基础。本节将描述如何识别数据是否是正态分布,如果针对不同的数据类型采用其适用的变换方法,将其变换为正态分布。这些变换包括反正弦和反余弦变换、平方根变换、对数变换、Box-Cox变换等。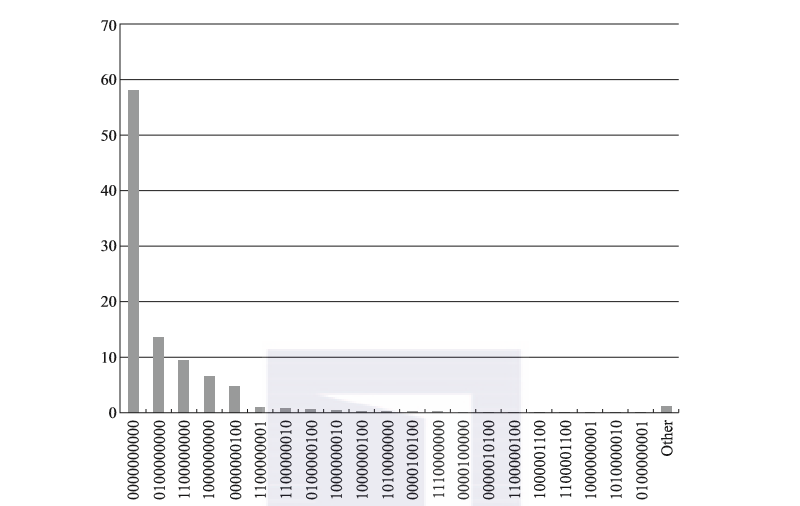
图2-17 由一个衍生字段代表原来10列数据的信息
(1)反正弦和反余弦变换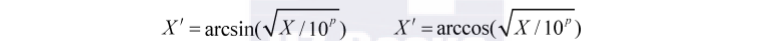
其中,p为正整数,这种变换适用于百分比形式的数据,通过把分布曲线的尾部拉长、中部压缩,使得弱负偏和弱正偏的不对称分布接近于正态分布。
(2)平方根变换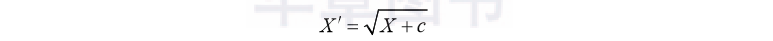
其中,c为常数,这种变换使正偏数据接近正态分布,常用于服从泊松分布的离散型数据。
(3)对数变换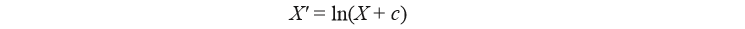
其中,c为常数,这种变换常用于服从对数正态分布的数据,对于正偏偏度很大的数据也很适用。由于这种分布是偏斜的,很可能出现零值,往往需要加上一个常数c。如果使c取值为0,那么要求因变量的所有取值都为非负数。
(4)Box-Cox变换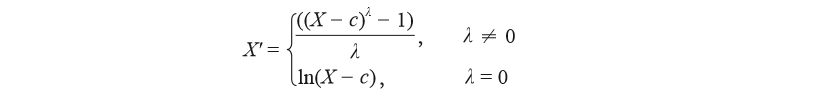
其中,c为常数,为了确保X-c大于0。Box-Cox变换可以被看作一个变换族,该变换族中有一个待定变换参数,取不同的值,就是不同的变换。当参数为0时是对数变换,参数为1/2时是平方根变换,参数为-1时是倒数变换。变换后的因变量服从正态分布。由此可以看出Box-Cox变换适用范围很广,其最大的优势在于将寻找变换的问题转化为一个估计参数的过程,通过极大似然估计来估计最优的参数。
对数据分布的挑剔,并不是所有的算法都是一致的。广义线性模型支持众多的分布类型,比如伽马分布、泊松分布、逆高斯分布、二项分布,多项分布等。线性回归算法是基于变量都是正态分布这样的假设来设计算法的,所以数据分布的改善能显著提高模型的精准度。
为了说明分布的变化如何改善模型效果,我们采用表2-12所示的员工个人信息数据集,通过salary、prevexp、jobtime、jobcat、gender、educ、minority等字段来预测salbegin
字段。
第一步,我们查看因变量的分布,如图2-18所示。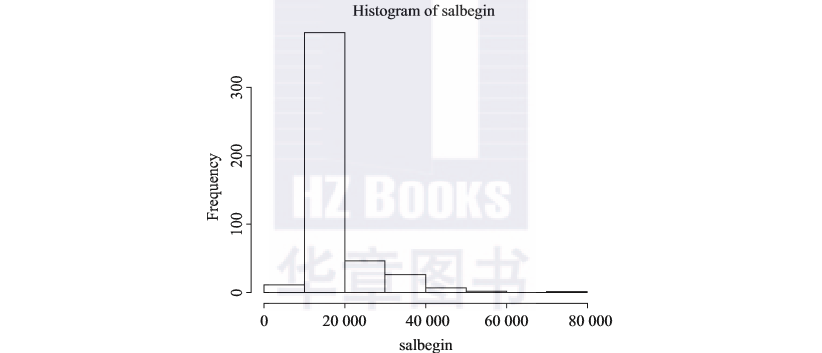
图2-18 因变量的分布
从图2-18中可以看出,因变量大致服从对数正态分布,且数据的取值集中于20000附近,其他区域几乎没有取值,说明数据的分布比较偏。
我们首先不对因变量进行转换,而是直接进行回归分析,代码如下。
得到的结果如下: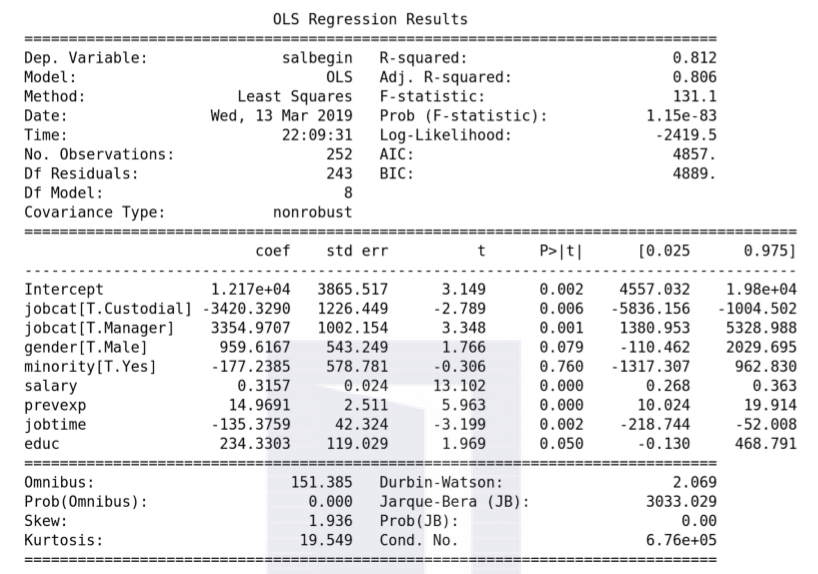
从Coefficients的结果可以看出,除了minority和gender的Male变量外,其他自变量都是显著的,对模型的估计贡献显著;然后从R-squared的结果可以看出,模型的拟合程度为0.812,修正后为0.806;最后从F检验的结果可以看出,模型整体是显著的。
如果对因变量做对数转换,会显著改变其分布,即从一个类似指数分布的状况改变为接近正态分布的状态,如图2-19所示。
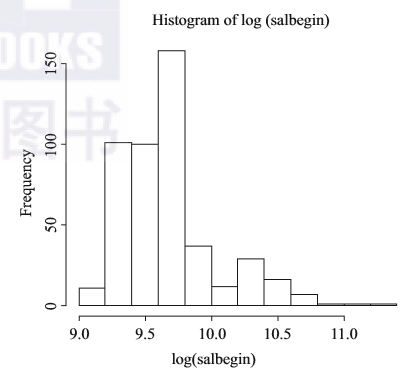
图2-19 因变量做对数转变后的分布
对因变量做指数变化后再建模,会发生什么样的变化?对数变化的效果到底如何?我们通过建模过程就可以看到,代码如下。
上述代码的执行结果如下: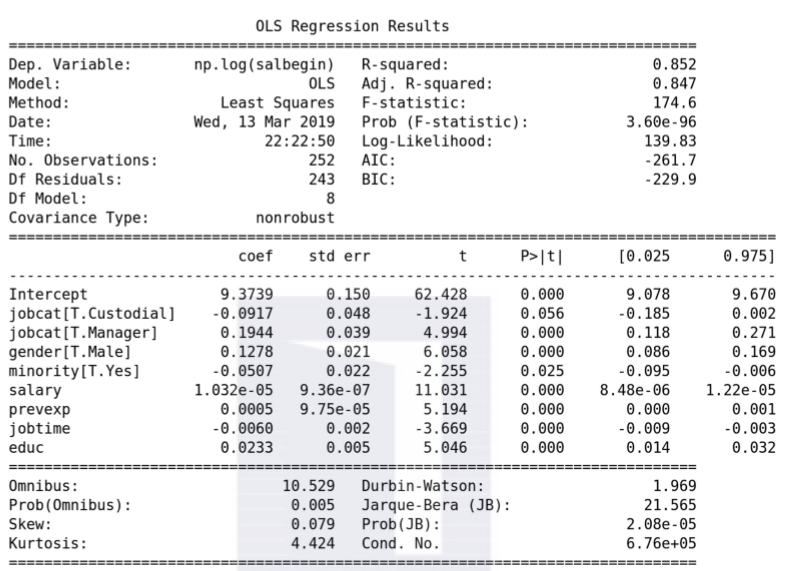
从Coefficients的结果可以看出,除了jobcat的Custodial变量外,其他自变量都是显著的,对模型的估计贡献显著;然后从R-squared的结果可以看出,模型的拟合程度为0.852,修正后为0.847;最后从F检验的结果可以看出,模型整体是显著的。
比较两个模型的结果,从中不难看出,模型的拟合度提高了。这说明变换后的数据能拟合出质量更高的模型,这得益于变换后的因变量更能服从正态分布。
2.2.3数据归约
数据归约(Data Reduction)是指在理解数据分析任务和数据本身内容的基础上,寻找依赖于发现目标的数据的有用特征,以缩减数据规模,从而在尽可能保持数据原貌的前提下,最大限度地精简数据量。数据归约主要从两个途径来实现:
1. 属性选择
属性选择就是通过有意而为之的动作,从大量的属性中筛选出与目标值(针对有监督的模型)或业务目标(针对无监督的模型)相关的属性,并将大量的不相关的数据摈弃。
这个过程既是一个主观判断的过程,也是一个需要通过技术手段计算相关性来选取的过程。主观判断体现了业务理解、业务经验和数据分析的经验。我们将在第6章专门讨论指标的选取过程。
2. 数据采样
从总体(Population/Universe)中确定抽样范围(Sampling Frame)并进行抽样,通过对样本的研究来估计或反映总体的特征,是经典的数据分析过程。
通过样本来估计总体特征的统计分析方法,或者通过对历史数据进行抽样并经过模型训练学习模式的数据挖掘,都是基于图2-20所示的思路进行的。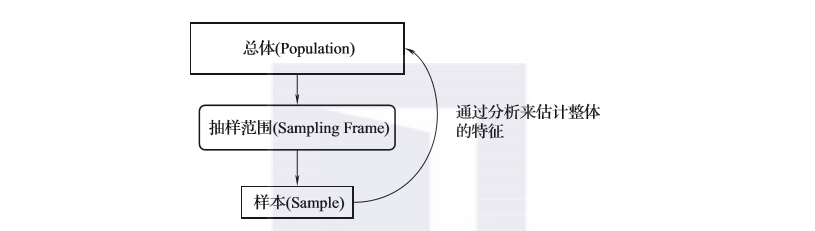
图2-20 数据采样的一般过程
在大数据时代,我们可以不需要通过样本来估计整体的特征,因为新的计算平台已经可以支持对海量数据进行快速处理。对均值不需要估计,直接计算即可。
但是,对于如预测、聚类分析等数据挖掘的场景,在大数据时代,采样仍然是必需的。在很多情况下,并不是样本越大(不论是列还是行)就意味着模型越好。笔者认为,经过深入的业务理解和数据理解后,针对具体的建模目标进行有效的衍生指标的加工才是最主要的。作者不否认很多时髦的算法能从数千个甚至数万个指标中快速计算并筛选出有效指标,如利用Lasso-logit算法在大数据平台上的实现,可以实现对近万个指标在数分钟内的快速筛选。这确实给指标的选取提供了极大的便利,貌似只要会将数据抽取出来并调用这些工具,大数据能很“智能”地做出计算和选择。其实,在数据挖掘的过程中,最为主要的是对业务的理解和衍生指标的加工。衍生指标往往能起到事半功倍的效果,它体现了建模的技巧,也体现了对问题的理解程度。
总的来说,抽样分为两种大的类型:典型抽样(Representative Samples)又称概率抽样(Probability Samples),抽样时没有人的主观因素加入,每个个体都具有一定的被抽中的概率;非典型抽样(Non-representative Samples)又称非概率抽样(Nonprobability Samples),抽样时按照抽样者的主观标准抽取样本,每个个体被抽中的机会不是来自本身的机会,而是完全来自抽样者的意愿。一个比较完整的抽样种类的图表如图2-21所示。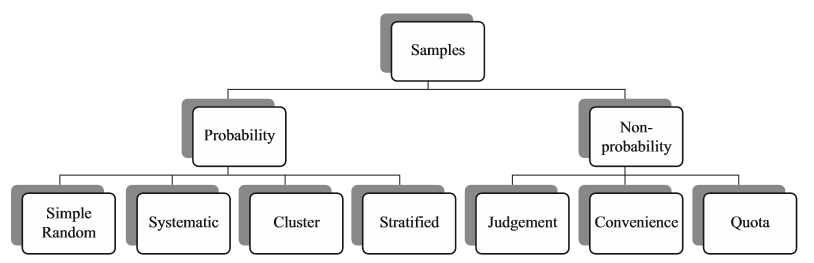
图2-21 典型的采样类型
概率抽样适用的场景是采用样本数据来体现整体的特征,包括以下几种:
- 简单随机抽样(Simple Random Sampling)。保证大小为n的每个可能的样本都有相同的被抽中的概率。例如,按照“抽签法”“随机表”法抽取数据对象。其优点是:随机度高,在特质较均一的总体中,样本具有很高的总体代表度。
- 系统随机抽样(Systematic Random Sampling)。将总体中的各单元先按一定顺序排列并编号,然后按照不一定的规则抽样。其中最常采用的是等距离抽样,即根据总体单位数和样本单位计算出抽样距离(相同的间隔),然后按相同的距离或间隔抽选样本单位。例如,从1000个电话号码中抽取10个访问号码,间距为100,确定起点后每100个号码抽一个访问号码。其优点是:操作简便,且与简单随机抽样相比,在一定条件下更能体现总体的特征。
- 分层随机抽样(Stratified Random Sampling)。把调查总体分为同质的、互不交叉的层(或类型),然后在各层(或类型)中独立抽取样本。例如,调查零售店时,按照其规模大小或库存额大小进行分层,然后在每层中按简单随机方法抽取大型零售店若干、中型零售店若干、小型零售店若干;调查城市时,按城市总人口或工业生产额分出超大型城市、中型城市、小型城市等,再抽出具体的各类型城市若干。从另一个角度来说,分层抽样就是在抽样之前引入一些维度,对总量的群体进行分层或分类,在此基础上再次进行抽样。
- 整群抽样(Cluster Sampling)。先将调查总体分为群,然后从中抽取群,对被抽中群的全部单元进行调查。例如,在人口普查时,可以按照地区将人口分为几个群体,然后选取某个群体,研究该群体内所有个体的特征,据此来推断该地区的人口特征。
非概率抽样都是按照抽样者的意愿来进行的,典型的方式有以下几种:
- 方便抽样(Convenience Sampling)。根据调查者方便选取的样本,以无目标、随意的方式进行。例如,街头拦截访问(看到谁就访问谁);个别入户项目(谁开门就访问谁)。
- 判断抽样(Judgment Sampling)。由专家判断而有目的地抽取他认为“有代表性的样本”。例如,社会学家研究某国家的一般家庭情况时,常以专家判断方法挑选“中型城镇”进行;在探索性研究中,如抽取深度访问的样本时,可以使用这种方法。
- 配额抽样(Quota Sampling)。先将总体元素按某些控制的指标或特性分类,然后按方便抽样或判断抽样选取样本元素。 配额抽样相当于包括两个阶段的加限制的判断抽样:在第一阶段需要确定总体中的特性分布(控制特征),通常,样本中具备这些控制特征的元素的比例与总体中有这些特征的元素的比例是相同的,通过第一步的配额,保证了在这些特征上样本的组成与总体的组成是一致的。在第二阶段,按照配额来控制样本的抽取工作,要求所选出的元素要适合所控制的特性。
在日常建模过程中,比较常用的抽样方法是简单随机抽样。在抽样结束后,可以通过一些简单、易用的方式来判断样本的某一特征是否体现了总体的特征。
图2-22中就是抽取了两个样本,并且比较了某个关键指标在两个样本、全集上的分布,据此来判断三者之间的差别。从图中可以看出,三者之间几乎没有多少差别,即可以认定样本可以用来代表全集的特征。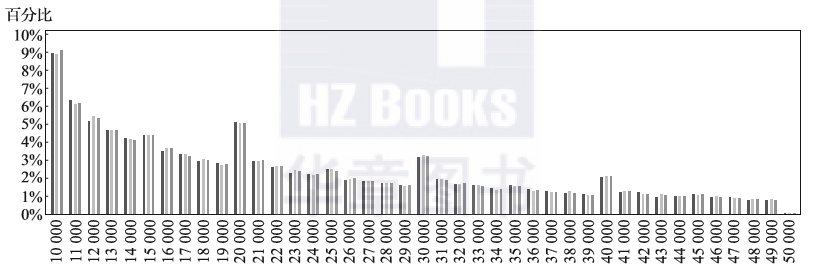
图2-22 两个样本、总体的关键指标的分布
2.3衍生指标的加工
在探索了数据的基本统计信息后,我们掌握了数据的分布特征等信息;接着又对数据做了预处理,过滤了缺失值和离群值,转变和处理了数据类型,提高了数据的质量。本节进一步对数据从字段上进行加工,从尺度、分布上进行变换,满足不同的业务和建模需要,变换后的字段更能满足模型需要,由此引出了本节的衍生指标的加工。
2.3.1衍生指标概述
所谓衍生指标(Derived Field)是指利用给定数据集中的字段,通过一些计算而加工产生一些新的指标。创建衍生指标是数据分析过程中最具创意的部分之一,是数据分析者必须具备的基本技能之一。衍生指标将人们的见解融入建模的过程中,使得模型的结论充分体现了业务、市场的重要特征。精心挑选的衍生指标能增强模型的可理解性和解释能力。
一般来说,对数据和变量进行加工和转换的主要目的是统一变量的数据尺度,使变量尽可能为正态分布,使变量之间的非线性关系转换为线性关系,使变量便于用简单自然的方式表示,帮助理解数据的特征,等等。不同的变换方法试图达到不同的目的,不同的模型对数据和变量的要求不同。譬如大多数多元统计方法要求变量的尺度一致,要求因变量服从正态分布。变量的变换一定要根据模型和业务的需要合理地进行。
衍生指标的创建主要体现了数据挖掘者对业务和目标的理解程度,体现了其解决问题的能力、对数据的敏感度和经验等。所以,衍生指标的创建在更多的时候是针对分析目标将既有指标进行加工。比如,银行的数据仓库针对每月的数据都进行了汇总,但是如何知道客户近期的活跃程度呢?一个简单的衍生指标就是“最近6个月平均每月的交易次数”,这就是一个很好的指标。这个指标的加工方式就是读取最近6个月的每月交易次数(很可能每个月都会对应于一张表),然后求一个平均值即可。
在进行数据分析的过程中,可以采用一个做法:将各个字段的数据都看作不断“说话”的部件。当面对很多部件时,就好比处在了一个嘈杂的环境中,数据分析者应当用一个平和的心态,通过查看数据分布、查看与目标变量的相关关系、加工衍生字段等方式,认真挑选这些字段。笔者一直认为,不论字段的数据质量到底如何,它们都是在不断地向我们“诉说”着什么,有些在诉说客户的价值,有些在诉说客户的行为,而数据分析者需要善于倾听和选择。笔者非常认可《数据挖掘技术》 中提到的衍生指标的加工方法介绍。在实际的项目中,这些方法非常实用。所以在接下来的小节中,我们参照了该书中的大纲安排,但内容来自笔者的实际项目总结。
2.3.2将数值转化为百分位数
数值体现被描述对象的某个维度的指标大小,百分比则体现程度。在有关银行的项目中,数据仓库中的大多指标都是在如实反映客户某指标的大小,如存款余额、理财余额等。这些指标在忠实地描述客观事实,利用它们可以轻易加工出业务含义明确的衍生指标,如客户的理财偏好程度:
理财偏好程度=同一时间窗口中资产余额均值(存款余额 + 理财余额 + …)×100%
该百分比越大,表明客户对理财的偏好程度越高。该衍生指标可以直接通过离散化对客户群体进行划分,也可以作为输入变量去构建各种模型(如预测、聚类等)。像这样的指标加工方式,在实际项目中可以灵活采用。
2.3.3把类别变量替换为数值
大多数算法在实际运算的过程中,都需要将分类型变量首先转换为数值型变量,然后才能进行计算。在本章的2.2.2小节中,也介绍了将分类型变量转换为数值型变量的方法:转为dummy虚拟变量,然后才参与模型计算。这种方法可以在调用算法之前作为数据预处理的步骤来进行,也可以直接交给算法去处理(算法的实现过程已经包含了该过程)。
但是从另一个方面来说,类别变量具有很重要的业务含义。比如,客户资产的类别:富裕客户,就是一个非常有实际业务指导意义的指标。有时,为了将连续型变量转换为分类型变量,这牵扯到分箱时的阈值划分,往往需要从数据分布和业务指导意义两个方面同时考虑。所谓富裕客户,一定是某些数值型变量达到一定的阈值,才会有这个标签。
在构建模型之前,最好不要将一些数值型变量转化为分类型变量。这会很大程度上伤害模型的性能。图2-23所示就是一个用SAS决策树算法生成的模型结果。如果在建模之前,我们生硬地将字段“Has_Bad_Payment_Re…”离散化,其结果在很大的程度上不会是以0.5作为阈值,那么该字段就不会那么重要(决策树的第二级节点),它的重要性很可能就会被别的字段所代替而导致我们得不到非常有用的业务规则,模型的性能也会显著下降。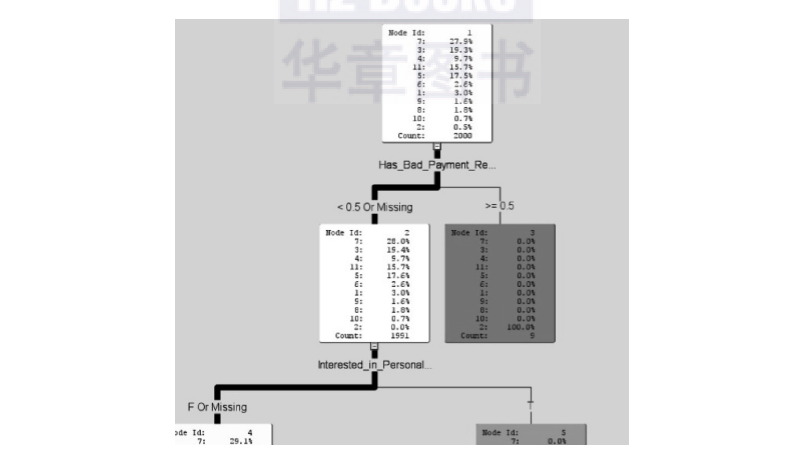
图2-23 一个SAS决策树算法生成的模型结果
从实际业务指导的角度来看,分类型变量的易用性远远大于数值型变量。从模型算法的角度来看,采用数值型的指标会显著提高模型的性能。针对“富裕客户”这样的指标值,在建模时为模型性能考虑,最好是将其代表的数值直接使用而摈弃分类型变量。
2.3.4多变量组合
多变量组合去计算出一个新的指标,是非常常用的衍生指标的计算方式,如针对银行客户的信用评级指数: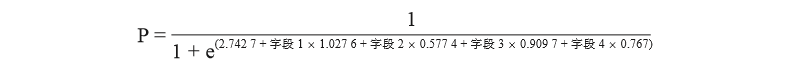
其中,字段1至字段4是一些既有的字段;P则是通过一系列的计算和分析,最终确定这些字段的组合方式得出的综合指标。在笔者最近进行的一个数据分析项目中,我们首先使用回归算法确定目标值与自变量之间的线性关系,这个关系体现了“什么样的投入会导致什么样的结果”: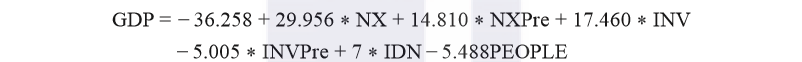
上述公式其实也是线性回归算法通过训练而得到的“模式(Pattern)”。根据这个公式,将其中一个自变量作为因变量,而原来的因变量变为自变量,来反推“当要达到预期的某个值时,需要多少投入”: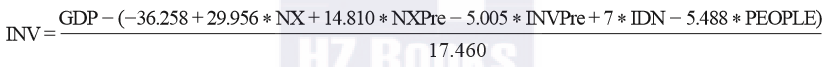
这是一个典型的goal seek过程,只是“需要多少投入”这样的结果完全可以作为一个新的衍生字段被计算出来。
在金融行业非常关注客户的“未来价值”,不同的价值给银行带来的收益也会大不相同。未来价值由很多方面来决定,如客户所从事的行业、教育程度、目前的资产、年龄、地区、家庭的经济状况等。这些数据很多是银行所不具备的,但是其可以借助一个比较简单的方式来估算:
这是一个没有严格数学含义的衍生指标,并且只能处理年龄在[25,60]区间以内的客户。但是该指标的业务含义却比较清晰:未来价值与客户当前年龄和当前的资产余额有很大的关系,该算法得到的结果值越大,表现出客户的未来价值越大;该值越小,客户的未来价值越小。
2.3.5从时间序列中提取特征
时间序列数据是指在不同时间点上收集到的数据,这类数据反映了某一事物、现象等随时间的变化状态或程度。设备的监控数据、温度随时间的变化、股票大盘随时间的波动等都是典型的时间序列数据。针对时间序列数据,有很多的专用算法可以用来做分析,如差分自回归移动平均模型(ARIMA)。
在应用非专门处理时间序列的算法时,有时需要从时间序列数据中提取一些典型有用的数据作为一个变量输入。比如,在预测性维护的场景中,设备是否需要维护或是否会出现故障的模型训练,需要将设备监控的数据做一些转换,作为预测模型的预测变量。如图2-24所示,可以将出现故障前兆的异常数据进行计数,或者通过计算方差的大小来体现指标的变化幅度,作为体现设备状态的典型指标来预测目标变量的取值。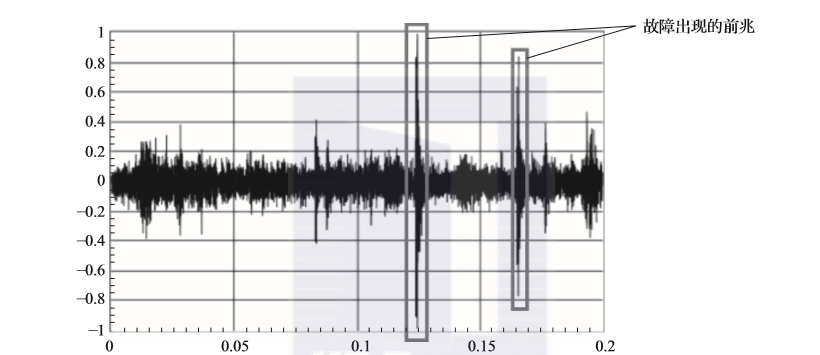
图2-24 监控信息中包含故障出现的前兆
